
Basic Operation
Particle motion is followed using a fourth-order, individual-timestep ``Hermite'' predictor-corrector scheme (Makino and Aarseth 1992). Briefly, during a time step, particle positions and velocities are first predicted to fourth order using the known acceleration and ``jerk'' (time derivative of the acceleration), the new acceleration and jerk are computed, and the motion is then corrected using the additional derivative information thereby obtained. Schematically, if pos, vel, acc, and jerk represent position, velocity, acceleration, and jerk at some time t, and the desired time step is dt, prediction consists of
pred_pos = pos + dt * (vel + (dt/2) * (acc + (dt/3) * jerk));
pred_vel = vel + dt * (acc + (dt/2) * jerk);
The acceleration and jerk are then recalculated at the predicted time,
using pred_pos and pred_vel. Finally, a correction
is based on the estimated higher-order derivatives:
a3 = 2 * (acc - pred_acc) + dt * (jerk + pred_jerk);
a2 = -3 * (acc - pred_acc) - dt * (2 * jerk + pred_jerk);
where
a2 = a'' * dt*dt / 2 (a = acc, a' = jerk)
a3 = a''' * dt*dt*dt / 6
so
pos = pred_pos + (a3/20 + a2/12) * dt * dt;
vel = pred_vel + (a3/4 + a2/3) * dt;
A single integration step in kira thus proceeds as follows:
Log Output
The format of a snapshot is described in the internals section. The standard log output presently consists of
Tree Structure
As discussed in more detail in the structure section, an N-body system in Starlab is represented as a linked-list structure, in the form of a mainly ``flat'' tree, individual stars being the ``leaves.'' The tree is flat in the sense that single stars (i.e. stars that are not members of any multiple system) are all represented by top-level nodes, having the root node as parent. Binary, triple, and more complex multiple systems are represented as binary trees below their top-level center of mass nodes. The tree structure determines both how node dynamics is implemented and how the long-range gravitational force is computed.
The motion of every node relative to its parent node is followed using the Hermite predictor-corrector scheme described above. The use of relative coordinates at every level ensures that high numerical precision is maintained at all times, even during very close encounters.
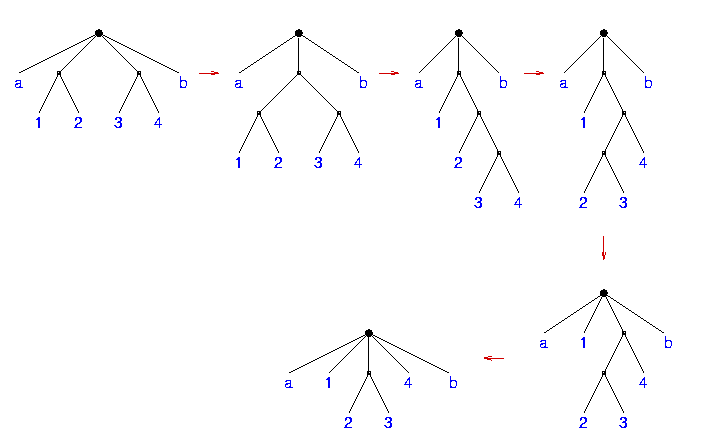
The tree evolves dynamically according to simple heuristic rules: particles that approach ``too close'' to one another are combined into a center of mass and binary node; and when a node becomes ``too large'' it is split into its binary components. These rules apply at all levels of the tree structure, allowing arbitrarily complex systems to be followed. The terms ``too close'' and ``too large'' are defined by command-line variables, as described below. The tree rearrangement corresponding to a simple three-body ``exchange'' encounter is:

How the acceleration (and jerk) on a particle or node is computed depends on its location in the tree. Top-level nodes feel the force due to all other top-level nodes in the system. Forces are computed using direct summation over all other particles in the system; no tree or neighbor-list constructs are used. (The integrator is designed specifically to allow efficient computation of these forces using GRAPE hardware, if available.) Nearby binary and multiple systems may be resolved into their components, as necessary.
The internal motion of a binary component is naturally decomposed into two parts: (1) the dominant contribution due to its companion, and (2) the perturbative influence of the rest of the system. (Again, this decomposition is applied recursively, at all levels in a multiple system.) Since the perturbation (gamma) drops off rapidly with distance from the binary center of mass, in typical cases only a few near neighbors are significant perturbers of even a moderately hard binary. These neighbors are most efficiently handled by maintaining lists of perturbers for each binary, recomputed at each center of mass step, thereby greatly reducing the computational cost of the perturbation calculation:

A further efficiency measure is the imposition of unperturbed motion for binaries whose perturbation falls below some specified value. Unperturbed binaries may be followed analytically for many orbits as strictly two-body motion; they are also treated as point masses, from the point of view of their influence on other stars. Because unperturbed binaries are followed in time steps that are integer multiples of the orbit period, we can relax the perturbation threshold for unperturbed motion, relative to that for a perturbed step, as illustrated in the diagram. Perturbed binaries are resolved into their components, both for purposes of determining their center of mass motion and for determining their effect on other stars. Unperturbed treatments of multiple systems also are used, based on empirical studies of the stability of their internal motion.
Escaper Removal
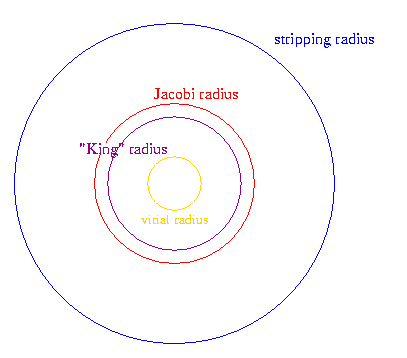
Stars are removed (``stripped'') from the system when they exceed a specified distance from the cluster center of mass (or density center). For systems without an imposed Galactic tidal field, this stripping radius is arbitrary. For systems with a tidal field, the stripping radius is more usually tied to the Jacobi radius of the cluster. The Jacobi radius (governed by the imposed tidal parameters) may or may not have anything to do with the ``King'' radius -- the cutoff radius of an initial King model. Typical relationships between these radii are shown below:
Command-line Parameters
The behavior of kira is controlled by its command-line parameters. As with all Starlab tools, a list of parameters may be obtained by typing
kira --help
The (excessively long) result is
Starlab version 3.4
program created ...
source file ...
kira: Hermite N-body integrator with evolving hierarchical tree
structure, stellar and binary evolution, and an external
tidal field.
Basic options are as follows. Default values for a new simulation are
indicated in square brackets. For restart (continuation of a previous
kira calculation), the defaults for many options [*] are determined from
the input snapshot, making it possible to continue a run without having
to re-specify all the command-line parameters previously used. (These
new defaults may still be overridden on the command line, of course.)
Some options typically having to do with initial setup may be overridden
by data from the input snapshot (if present), as noted below. Kira may
also turn *on* some options (the B, G, Q, S, and u settings) if they
were turned on in the previous run, but are not specified on the current
command line. To prevent this, use the "-o" switch.
The first page of log output gives complete information on parameter
settings adopted and modifications made during initialization. In case
of doubt, read the log file!
Options: -a specify accuracy parameter [0.1][*]
-B turn on binary evolution [off][*]
-c include comment [none]
-C specify GRAPE release interval, in seconds [15]
-d specify log output interval [0.25][*]
-D specify snapshot interval [end of run]
-e specify softening length [0][*]
-E use exact calculation [false]
-f specify close-encounter distance [1 --> 1/N][*]
-F specify tidal field type (0 = none, 1 = point-mass,
2 = isothermal, 3 = disk)
[0 if -Q not set; 1 otherwise][*]
-g specify hysteresis factor [2.5][*]
-G specify initial stripping radius [none][*]
-h specify stellar-evolution time step [0.015625 = 1/64][*]
-I specify (re)initialization timescale [1][*]
-J specify Jacobi radius [none][*]
-k specify perturbation factor [1.e-7][*]
-L specify CPU time limit, in seconds [none]
-M specify initial total mass, in solar masses
[none; take from input snap if present]
-n stop at specified number of particles [10]
-N specify frequency of CPU check output [25000]
-O save (and overwrite) extra snapshot at each output [no]
-q specify initial virial ratio [0.5]
-o prevent kira from overriding some settings (BGQSu)
based on input snapshot data [allow]
-Q use tidal field [none][*]
-r specify initial virial radius in code units
[1; take from input snap if present]
-R specify initial virial radius, in pc
[none; take from input snap if present]
-s specify random seed [take from system clock]
-S turn on stellar evolution [off][*]
-t specify time span of calculation [10]
-T specify initial virial time scale, in Myr
[none; take from input snap if present]
-u toggle unperturbed multiple motion [disabled][*]
-U toggle all unperturbed motion [enabled][*]
-v toggle "verbose" mode [on]
-X specify escaper removal timescale [reinit][*]
-y specify stellar encounter criterion
[0 N-body units or solar radii][*]
-z specify stellar merger criterion [0 stellar radii][*]
-Z specify stellar tidal dissipation criterion
[0 stellar radii][*]
As a convenient shorthand, any "dt" interval specified less than zero
is interpreted as a power of 2, i.e. "-d -3" sets dt_log = 0.125.
Many of the above options are fairly self-explanatory. For reference (in the choice of default units) ``standard'' N-body units (see Heggie and Mathieu, 1986) are typically defined so that the length and time scales of the system are unity, and the energy is -1/4.
A few specifics: