
A giant trap has been set deep underground to catch a few of the neutrinos that theory predicts should be pouring out of the sun. Their capture would prove that the sun runs on thermonuclear power.

Most physicists and astronomers believe that the sun's heat is produced by thermonuclear reactions that fuse light elements into heavier ones, thereby converting mass into energy. To demonstrate the truth of this hypothesis, however, is still not easy, nearly 50 years after it was suggested by Sir Arthur Eddington. The difficulty is that the sun's thermonuclear furnace is deep in the interior, where it is hidden by an enormous mass of cooler material. Hence conventional astronomical instruments, even when placed in orbit above the earth, can do no more than record the particles, chiefly photons, emitted by the outermost layers of the sun.
Of the particles released by the hypothetical thermonuclear reactions in the solar interior, only one species has the ability to penetrate from the center of the sun to the surface (a distance of some 400,000 miles) and escape into space: the neutrino. This massless particle, which travels with the speed of light, is so unreactive that only one in every 100 billion created in the solar furnace is stopped or deflected on its flight to the sun's surface. Thus neutrinos offer us the possibility of ``seeing'' into the solar interior because they alone escape directly into space. About 3 percent of the total energy radiated by the sun is in the form of neutrinos. The flux of solar neutrinos at the earth's surface is on the order of 1011 per square centimeter per second. Unfortunately the fact that neutrinos escape so easily from the sun implies that they are difficult to capture.
Nevertheless, within the past year a giant neutrino trap has begun operating in a rock cavity deep below the surface in the Homestake Mine in Lead, S.D. The neutrino trap is a tank filled with 100,000 gallons of tetrachloroethylene (C2Cl4), an ordinary cleaning fluid. The experiment is being conducted by Raymond Davis, Jr., of the Brookhaven National Laboratory, with the assistance of Kenneth C. Hoffman and Don S. Harmer. In 1964 Davis and I showed that such an experimental test of the hypothesis of nuclear burning in stars was feasible. The idea was strongly supported by, among others, William A. Fowler of the California Institute of Technology, Richard W. Dodson, chairman of the Brookhaven chemistry department, and Maurice Goldhaber, the director of Brookhaven. Subsequently the Homestake Mining Company contributed valuable technical help.
The initial results published by Davis and his co-workers have left astronomers and astrophysicists somewhat puzzled because the neutrino flux rate seems low. It is less than half the theoretical value one obtains by assuming certain ``standard'' values for quantities used in constructing theoretical models of the solar interior. I shall discuss the range of theoretical predictions later. The important initial fact is that one can now use the results of the experiment to improve our knowledge of the sun's thermonuclear furnace.
Neutrinos were first suggested as hypothetical entities in 1931 after it was noted that small amounts of mass seemingly vanish in the radioactive decay of certain nuclei. Wolfgang Pauli suggested that the mass was spirited away in the form of energy by massless particles, for which Enrico Fermi proposed the name neutrino (``little neutral one''). Fermi also provided a quantitative theory of processes involving neutrinos. In 1956 Frederick Reines and Clyde L. Cowan, Jr., succeeded in detecting neutrinos by installing an elaborate apparatus near a large nuclear reactor. Such a reactor emits a prodigious flux of antineutrinos produced by the radioactive decay of fission products. For purposes of demonstrating a particle's existence, of course, an antiparticle is as good as a particle.
In the late 1930's Hans A. Bethe of Cornell University followed up Eddington's 1920 suggestion of the nuclear origin of the sun's energy and outlined how the fusion of atomic nuclei might enable the sun and other stars to shine for the billions of years required by the age of meteorites and terrestrial rocks. Since the 1930's the birth, evolution and death of stars have been widely studied. It is generally assumed that the original main constituent of the universe was hydrogen. Under certain conditions hydrogen atoms presumably assemble into clouds, or protostars, dense enough to contract by their own gravitational force. The contraction continues until the pressure and temperature at the center of the protostar ignite thermonuclear reactions in which hydrogen nuclei combine to form helium nuclei. After most of the hydrogen has been consumed, the star contracts again gravitationally until its center becomes hot enough to fuse helium nuclei into still heavier elements. The process of fuel exhaustion and contraction continues through a number of cycles.
The sun is thought to be in the first stage of nuclear burning. In this stage four hydrogen nuclei (protons) are fused to create a helium nucleus, consisting of two protons and two neutrons. In the process two positive charges (originally carried by two of the four protons) emerge as two positive electrons (antiparticles of the familiar electron). The fusion also releases two neutrinos and some excess energy, about 25 million electron volts (MeV). This energy corresponds to the amount of mass lost in the overall reaction, which is to say that a helium nucleus and two electrons weigh slightly less than four protons. The 25 MeV of energy so released appears as energy of motion in the gas of the solar furnace and as photons (particles of radiant energy). This energy ultimately diffuses to the surface of the sun and escapes in the form of sunlight and other radiation.
 +)
generated in an atmospheric collision decays into a positive muon
(
+)
generated in an atmospheric collision decays into a positive muon
(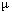 +) and a
``muon neutrino.'' High-energy muons are very penetrating and can knock protons
out of atomic nuclei well below the earth's surface. If such a proton entered
the neutrino detector, it could mimic the entry of a solar neutrino by
converting an atom of chlorine 37 (37Cl) into
an atom of radioactive argon 37 (37Ar).
+) and a
``muon neutrino.'' High-energy muons are very penetrating and can knock protons
out of atomic nuclei well below the earth's surface. If such a proton entered
the neutrino detector, it could mimic the entry of a solar neutrino by
converting an atom of chlorine 37 (37Cl) into
an atom of radioactive argon 37 (37Ar).
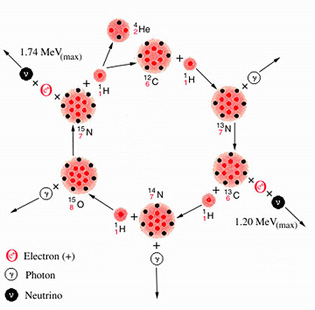
Bethe and C. F. von Weizäcker of
Germany independently proposed one
mechanism for assembling four protons into a helium nucleus. Because it
involved nuclei of carbon, nitrogen and oxygen it became known as the CNO
cycle [see illustration on the CNO Cycle]. The cycle starts with a nucleus of
ordinary carbon,  .
(The symbol specifies a nucleus containing
a total of 12
nucleons, of which six are protons and the rest neutrons.) Three protons
are added one at a time, culminating in a nitrogen nucleus containing eight
neutrons and seven protons (
.
(The symbol specifies a nucleus containing
a total of 12
nucleons, of which six are protons and the rest neutrons.) Three protons
are added one at a time, culminating in a nitrogen nucleus containing eight
neutrons and seven protons (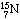 ).
With the addition of another proton a
reaction occurs in which two nuclei are produced:
).
With the addition of another proton a
reaction occurs in which two nuclei are produced:  (the original nucleus) and
(the original nucleus) and 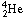 ,
which is ordinary helium.
,
which is ordinary helium.
In each cycle two neutrinos are emitted whose maximum energies are greater than 1 MeV. One comes from the radioactive decay of 13N and the other from the decay of 15O. (For simplicity I shall start omitting the subscripts indicating the number of protons in the nucleus.) The rates at which nuclear reactions in the CNO cycle occur in stars have been carefully studied over the past 20 years at the California Institute of Technology in the W. K. Kellogg Radiation Laboratory, first under the leadership of Charles C. Lauritsen and now of Fowler.
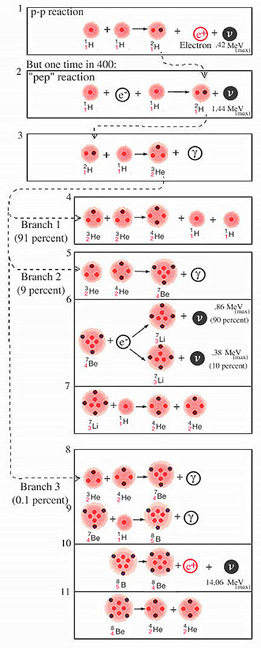
An altogether different series of nuclear reactions known as the proton-proton chain, also investigated 30 years ago by Bethe, can accomplish the same fusion of helium from four protons [see illustration on the Proton-Proton Chain]. In the first step of the chain two protons combine to form a deuteron, 2H. the nucleus of heavy hydrogen. The deuteron then combines with a proton to form a light helium nucleus, 3He. The next reaction can go in one of three directions. We estimate that in the sun's interior two nuclei of 3He combine to form an ordinary helium nucleus, 4He, with the release of two protons in about 91 percent of the cases. The other two possible branches, or routes, involve the formation of nuclei of lithium, beryllium and boron (7Li, 7Be, 8Be and 8B), which give rise eventually to two helium nuclei.
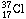 , an atom with 17 protons
and 20 neutrons. The other three chlorine atoms contain two less neutrons and
are designated
, an atom with 17 protons
and 20 neutrons. The other three chlorine atoms contain two less neutrons and
are designated 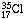 .
When a neutrino of the right energy
reacts with an atom of
.
When a neutrino of the right energy
reacts with an atom of 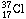 ,
it produces an atom of
,
it produces an atom of
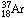 and an electron. The radioactive argon 37 is
allowed to build up for several months, then is removed by purging the tank
with helium gas. The argon is adsorbed in a cold trap and assayed for
radioactivity.
and an electron. The radioactive argon 37 is
allowed to build up for several months, then is removed by purging the tank
with helium gas. The argon is adsorbed in a cold trap and assayed for
radioactivity.
At the time Bethe first investigated the proton-proton chain there was little experimental information on the rates of the relevant nuclear reactions. Since then laboratories all over the world have provided the data for a detailed understanding of the chain and its several branches. At the low energies believed to exist in the solar furnace (a few thousand electron volts) the probability of the occurrence of any given reaction in the proton-proton chain is low and hence difficult to measure. Nevertheless, the experimental group at the Kellogg Laboratory, aided by a succession of able graduate students, has refined the difficult experiments to the point where most of the information necessary for predicting the rates of reactions in the proton-proton chain is now available.
Three of the reactions in the proton-proton chain are of special importance for solar-neutrino experiments. Referring again to the illustration on the Proton-Proton Chain, these are the basic proton-proton reaction [Reaction 1], the proton-electron-proton, or ``pep,'' reaction [2] and the decay of a radioactive isotope of boron, 8B [10]. All produce neutrinos but only the second and third produce neutrinos energetic enough to trigger a reaction in the tetrachloroethylene detector.
The proton-proton reaction is the slowest in the proton-proton chain, and hence it determines the overall rate at which energy is produced. Unfortunately the rate of the reaction is so slow that it cannot be measured in the laboratory; the ``weak'' force that governs this reaction is the same force that determines the interaction of neutrinos with matter. Over the years the rate of the reaction under stellar conditions has been estimated by a number of theorists. Last year I collaborated with Robert M. May of the University of Sydney in making a new estimate that we believe is accurate to within 5 percent.
The pep reaction differs from the basic proton-proton reaction only in that it has a negative electron present initially rather than a positive electron present after the reaction. Its rate at solar densities and temperatures is even slower than the proton-proton reaction. May and I estimate that the pep reaction occurs 1/400th as often as the proton-proton reaction under solar conditions. The pep neutrinos, which are 3 1/2 times more energetic than the most energetic proton-proton neutrinos, should be barely detectable. As we shall see, their capture rate establishes the minimum rate compatible with the hypothesis that the sun has a thermonuclear furnace.
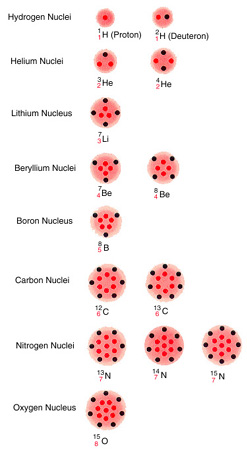
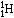 ,
whose nucleus
consists of a single proton. Four protons can be fused into a helium nucleus,
,
whose nucleus
consists of a single proton. Four protons can be fused into a helium nucleus,
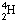 ,
by two principal mechanisms, one called the CNO cycle because it involves
carbon, nitrogen and oxygen nuclei (see illustration
on CNO Cycle) and the
other known as the proton-proton chain, which involves nuclei of helium,
lithium, beryllium and boron (see illustration on the Proton-Proton Chain). Protons are
represented by colored dots, neutrons by black dots, arranged in arbitrary
patterns. Other particles involved in the reactions are electrons (positive
and negative), photons and neutrinos.
,
by two principal mechanisms, one called the CNO cycle because it involves
carbon, nitrogen and oxygen nuclei (see illustration
on CNO Cycle) and the
other known as the proton-proton chain, which involves nuclei of helium,
lithium, beryllium and boron (see illustration on the Proton-Proton Chain). Protons are
represented by colored dots, neutrons by black dots, arranged in arbitrary
patterns. Other particles involved in the reactions are electrons (positive
and negative), photons and neutrinos.
The third reaction of special importance, the decay of radioactive boron, 8B, produces the most energetic neutrinos of all: they have a maximum of 14.06 MeV, or nearly 10 times the maximum energy of the pep neutrinos. The 8B is formed when beryllium, 7Be, adds a proton, a reaction [9] that occurs in a rare branch of the proton-proton chain. This branch begins with the fusion of light and heavy helium nuclei, 3He and 4He, which form 7Be. In 1958 Harry D. Holmgren and R. L. Johnson of the Naval Research Laboratory discovered that this reaction is significantly faster than had been thought. It proceeds at a rate of about once for every 1,000 occurrences in the sun of the more probable 3He-plus-3He reaction. Immediately following this discovery Fowler and A. G. W. Cameron suggested that the decay of 8B might produce a detectable flux of solar neutrinos. I subsequently made some calculations that showed that the capture probability for the energetic neutrinos emitted by 8B was 18 times larger than had been previously estimated. On the basis of this calculation Davis suggested in 1964 the experiment eventually located at the Homestake mine.
We are now ready to ask: How can tetrachloroethylene serve as a detector of solar neutrinos? Some 20 years ago Bruno M. Pontecorvo, then at the Chalk River Nuclear Laboratories in Canada, pointed out that an isotope of chlorine, 37Cl, could capture a neutrino and be transformed into an isotope of the rare gas argon, 37Ar, with the release of an electron. Subsequently the suggestion was discussed in detail by Luis W. Alvarez of the University of California at Berkeley. On the basis of Alvarez' discussion Davis and Harmer attempted to observe the argon produced by antineutrinos from the decay of fission products. (They placed a 3,000-gallon detector near a nuclear reactor.)
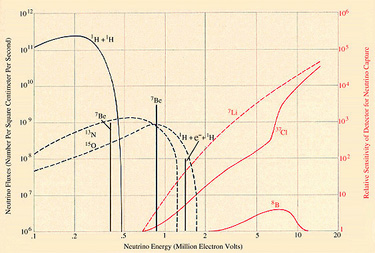
The argon isotope produced by neutrino capture is unstable and reverts to 37Cl by capturing one of its own orbital electrons. Fifty percent of a sample of 37Ar atoms will undergo such a transformation in about 35 days. The decay process shakes loose a low-energy electron from the argon atom, and this electron can be detected by counters placed around the sample. The detection of such electrons would be a sign that a few 37Cl atoms had been transformed into 37Ar atoms by neutrinos. The minimum neutrino energy for this reaction is .81 MeV [see illustration on Spectrum of Solar-Neutrino Energies].
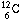 ,
as a catalyst, which is regenerated. Neutrinos are released in the second
and fifth steps of the cycle. Because they share energy with the positive
electrons that are emitted simultaneously, the neutrinos emerge with a spectrum
of energies, whose maximum values
are indicated. Unfortunately many of the neutrinos from the cycle lack the
energy to trigger chlorine-37 detection system, which has a threshold of .81
million electron volt (MeV).
,
as a catalyst, which is regenerated. Neutrinos are released in the second
and fifth steps of the cycle. Because they share energy with the positive
electrons that are emitted simultaneously, the neutrinos emerge with a spectrum
of energies, whose maximum values
are indicated. Unfortunately many of the neutrinos from the cycle lack the
energy to trigger chlorine-37 detection system, which has a threshold of .81
million electron volt (MeV).
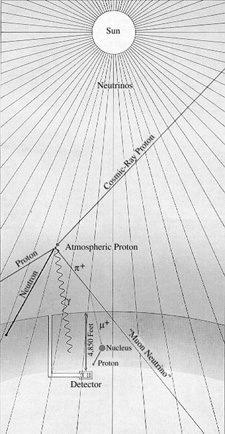
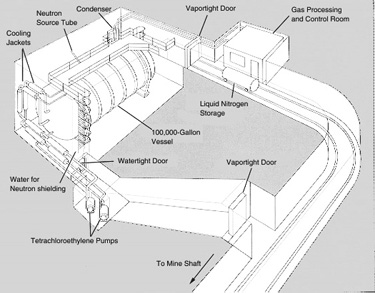
For the detection scheme to work one must end up with at least a dozen or so 37Ar atoms. Calculations suggested that a practical experiment would require a detector consisting of 100,000 gallons of a chlorine-containing fluid, such as tetrachloroethylene. (In natural chlorine a fourth of the atoms are the isotope 37Cl.) In the experiment designed by Davis and his colleagues this volume of tetrachloroethylene is contained in a tank 20 feet in diameter and 48 feet long, located 4,850 feet underground [see illustration on the Solar-Neutrino Detector].
Why underground? The answer is that the detector must be shielded from the shower of subnuclear particles of all kinds produced when cosmic rays (chiefly high-energy protons) crash into the earth's atmosphere [see illustration on the Deep-Mine Location]. Several reactions triggered by such particles could simulate the reaction Davis was looking for, but it is particularly important to exclude free protons from the tank because if 37Cl absorbs a proton it can be converted into 37Ar by the release of a neutron. Although one does not expect free protons to penetrate many feet of rock, muons produced by cosmic rays are very penetrating and can cause reactions that will release protons many feet below the surface. As a shield against neutrons, which are another hazard, the entire tank can be surrounded by water.
The tankful of tetrachloroethylene is exposed to the flux of neutrinos from the sun for several months to allow the atoms of 37Ar to accumulate. (I might add that the flux of neutrinos from the rest of the universe presumably bears roughly the same relation to the solar-neutrino flux as starlight does to sunlight; hence it can be ignored.) The 37Ar formed by neutrino capture is then removed from the bulk of the liquid by bubbling large quantities of helium gas through the system. About 10 cubic feet of helium is circulated through the tank per minute. The argon is separated from the helium by absorbing it in a charcoal trap maintained at the temperature of liquid nitrogen (77 degrees Kelvin). The efficiency of the extraction procedure is determined in each experiment by adding to the 100,000 gallons of tetrachloroethylene a known amount (less than a cubic centimeter) of 36Ar, a rare nonradioactive isotope of argon. Davis finds that purging the tank for 22 hours with helium will usually recover 95 percent of the 36Ar.
The argon that is finally removed from the tank Consists primarily of 36Ar, deliberately inserted, together with two other isotopes: a few atoms of 37Ar produced by solar neutrinos and a tiny amount of the ordinary nonradioactive isotope of argon, 40Ar, that might have leaked into the tank from the air. After the sample of argon is purified chemically it is placed in a small counter holding about .5 c.c. of gas. The counter is made small to minimize its exposure to cosmic rays or other unwanted particles. It is protected from outside radiations by a series of shields and by large counters that signal when something has penetrated the outer defenses. The shape of each pulse occurring in a counter is photographed, and the pertinent data (such as the time of occurrence and the energy of the pulse) are stored on computer tape.
Ray Davis tells me that the experiment is simple (``Only plumbing'') and that the chemistry is ``standard.'' I suppose I must believe him, but as a nonchemist I am awed by the magnitude of his task and the accuracy with which he can accomplish it. The total number of atoms in the big tank is about 1030. He is able to find and extract from the tank the few dozen atoms of 37Ar that may be produced inside by the capture of solar neutrinos. This makes looking for a needle in a haystack seem easy.
Let me explain now how I calculated the probability that a solar neutrino that enters the tank of tetrachloroethylene will be captured by one of the 37Cl atoms. The fraction of neutrinos with energies in any given range can be determined for a particular neutrino source from laboratory experiments. One can also calculate with the aid of Fermi's theory of neutrino processes the likelihood that an atom of 37Cl will capture a neutrino of a particular energy. From a threshold probability of zero for a neutrino of .81 MeV the relative capture probability rises to 100 for a neutrino of 4 MeV, to 1,000 for a neutrino of 7 MeV and to 30,000 for a neutrino of 14 MeV. Thus the probability of capturing a 14-MeV neutrino from 8B decay is some 3,000 times higher than the probability of capturing a 1.4-MeV neutrino from the pep reaction.
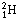 ,
produced in these two reactions fuse with protons to form a light isotope of
helium,
,
produced in these two reactions fuse with protons to form a light isotope of
helium, 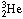 (3). At this point the proton-proton chain breaks into three
branches. A few barely detectable neutrinos are produced in the second branch
by Reaction 6. The most energetic neutrinos are released (10) in the rare
branch involving boron 8.
(3). At this point the proton-proton chain breaks into three
branches. A few barely detectable neutrinos are produced in the second branch
by Reaction 6. The most energetic neutrinos are released (10) in the rare
branch involving boron 8.
Moreover, the neutrinos from the decay of 8B can do something that none of the other solar neutrinos can. They are so energetic they produce a 37Ar nucleus that is in an excited state. This means that the nucleus has more internal energy than it would have in the ground, or normal, state. The significance of this is that favorable nuclear transitions can be caused by 8B neutrinos that are not possible with the lower-energy neutrinos. The most important excited state of 37Ar is quite similar to the ground state of 37Cl; it is the nuclear analogue of the ground state of 37Cl. The consideration of excited states led to an accurate determination of the probability that 37Cl will capture an 8B neutrino.
The chain of argument is based on the symmetry properties of nuclei containing
the same number of nucleons and proceeds as follows. The nucleus
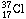 (I shall
again indicate the protons by subscripts) should behave very much like the
calcium nucleus
(I shall
again indicate the protons by subscripts) should behave very much like the
calcium nucleus 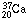 ,
which was unknown when I made my nuclear model. The model
predicted that
,
which was unknown when I made my nuclear model. The model
predicted that 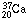 should decay within 130 milliseconds, on the average, into
an excited potassium nucleus
should decay within 130 milliseconds, on the average, into
an excited potassium nucleus 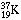 plus a positive electron and a neutrino. In
a nuclear sense this is exactly analogous to the capture of a neutrino by
plus a positive electron and a neutrino. In
a nuclear sense this is exactly analogous to the capture of a neutrino by
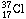 ,
producing
,
producing 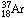 plus an electron.
plus an electron.
About a year later the isotope 37Ca was observed, and its decay rate was found to be within 25 percent of the value predicted. More important, subsequent measurements by Arthur M. Poskanzer and his associates at Brookhaven determined the fraction of decays of 37Ca that lead to various excited states of 37K. These were precisely the results needed to calculate the neutrino-capture rate of 37Cl with an accuracy of better than 10 percent.
It is convenient to introduce a special unit to express the neutrino-capture rate in solar-neutrino experiments. The unit is the ``solar-neutrino unit,'' or SNU (which we pronounce ``snew''). One SNU equals 10-36 capture per second per target atom. This implies that an atom of 37Cl would have to wait 1036 seconds, or roughly 10 billion billion times the age of the observable universe, before capturing a neutrino. Of course, in the 100,000-gallon tank, which contains about 2 x 1030 atoms of 37Cl, the average waiting time for a single capture when the rate of capture equals 1 SNU is only 5 x 105 seconds, or about six days per capture.
Let us now see how the capture rate in SNU's varies, depending on which reaction, or combination of reactions, one thinks is responsible for the sun's thermonuclear energy [see illustration on Predicted Neutrino Capture Rates]. If the CNO cycle is the dominant source of the sun's energy, I estimate that the capture rate is 35 SNU. On the other hand, if the sun derives its energy from the proton-proton chain, as most theorists now believe, the problem of predicting the capture rate becomes difficult. One has to calculate precise models for the interior of the sun and estimate the average temperature of the solar furnace to an accuracy of .1 percent in order to predict the capture rate to an accuracy of a few percent, which is our usual aim.
The equations needed for such models have been known for some time. The first equation states that the gravitational attraction of the solar gas is balanced at each point in the sun by the thermal pressure of moving gas particles and by the pressure of radiation (photons). The second equation states that the total energy emitted by the sun represents the sum of all the energy released by the individual thermonuclear reactions. Finally, there is an equation that describes how energy is transported from the interior to the surface of the sun. This equation requires one to assume a particular chemical composition for the solar material so that one can estimate its opacity (that is, how strongly it impedes photons trying to reach the surface). We make the conventional assumption that the abundances observed spectroscopically at the surface of the sun are the same today as when the sun was formed. This assumption has been questioned, however, by Icko Iben, Jr., of the Massachusetts Institute of Technology, who has pointed out that our calculated primordial helium abundance for the sun is different from the abundance observed in some other stars. The situation is still somewhat unclear, although we are encouraged by the fact that our models enable us to calculate correctly the abundance of helium atoms observed in those cosmic rays that come from the sun.
All the quantities mentioned-pressure, reaction rates and opacity-must be computed at temperatures some 50,000 times higher and densities 100 times greater than those normally encountered on the earth. The central temperature of the sun is believed to be about 15 million degrees Kelvin and the central density about 150 grams per cubic centimeter. The calculation of reasonably accurate values for the opacity of stellar material alone has taken years of effort by Arthur N. Cox and his associates at the Los Alamos Scientific Laboratory.

The calculation of a detailed solar model requires about 10 minutes on a modern high-speed computer. The first calculations of solar-neutrino flux based on detailed models of the sun were published in 1963 by Fowler, Iben, Richard L. Sears and myself. Our 1963 model indicated that the capture rate would be about 50 SNU. Subsequent pioneering work was done by Sears. Since then I have been trying to estimate and reduce the uncertainties in our calculations that arise from imperfectly known parameters. This work has been carried out with a number of able collaborators, including most recently my wife Neta Bahcall, Giora Shaviv and Roger Ulrich. Our best solar model, using what we consider the most likely set of parameters for the proton-proton chain, predicts a capture rate of only 6 SNU-smaller by nearly a factor of 10 than predicted by our 1963 model. The main difference between our 1963 estimate and the present one results from improved measurements of nuclear reaction probabilities and of the sun's composition. (The composition work was done by D. Lambert and A. Warner of the University of Oxford.) We estimate that the uncertainty in the new value of the capture rate is roughly a factor of two or three.
About 80 percent of the expected rate of 6 SNU represents neutrinos from the decay of radioactive boron, 8B, produced when 7Be captures a proton. The parameter describing the rate of this reaction at solar temperatures is usually designated S17 (1 stands for proton and 7 for 7Be). The ``standard'' value for S17 was determined in 1968 by Peter D. Parker of Yale University, and is the value that gives 6 SNU. An indirect determination of S17, yielding a lower value, had been made a few years earlier at Cal Tech by Thomas A. Tombrello. He made use of reactions involving 7Li and neutrons instead of 7Be and protons. If this lower value of S17 is used, the estimated capture rate falls to 3 SNU. Independent of the uncertainty surrounding Sl7 and other parameters, my wife, Ulrich and I have established that the most general ideas concerning the solar interior predict a probable capture rate of between 1 and 3 SNU.
A minimum capture rate can be obtained by calculating the contribution from pep neutrinos alone. Regardless of what model one selects for the interior of the sun, the ratio of pep reactions to standard proton-proton reactions is in the ratio of about one to 400. Moreover, the observed luminosity of the sun determines the rate of the basic proton-proton reaction. Therefore the capture rate attributable to pep neutrinos is an absolute lower limit (with one imaginative exception that will be mentioned below) consistent with the hypothesis that fusion reactions make the sun shine. Calculations I have made with the help of my wife, Shaviv and Ulrich show that this minimum capture rate is .29 ± .02 SNU.
The results published last year by Davis and his co-workers show that the capture rate with 37Cl is probably less than 3 SNU. The experimental value clearly implies that less than 10 percent of the sun's energy is generated by the CNO cycle. It also implies that the value of 6 SNU, based on ``standard'' parameters for the proton-proton chain, is at least twice too high. This discrepancy of a factor of two has caused considerable excitement in the scientific community. As we have seen, however, the uncertainties in some parameters are large enough so that Davis' result does not imply a conflict with general ideas about the solar interior.
Nevertheless, several theorists have suggested ways to explain the apparent discrepancy. D. Ezer and Cameron of the National Aeronautics and Space Administration suggest that the inner parts of the sun have somehow been mixed with the outer parts, thus reducing composition differences attributable to nuclear reactions in the solar interior. Their idea has been investigated quantitatively by a number of workers, who have found that mixing can indeed significantly reduce the expected solar-neutrino flux. Their suggestion, however, has not been widely accepted because the required amount and duration of mixing are quite large.
The most imaginative idea has come from the U.S.S.R., where V. N. Gribov and Pontecorvo (who originally suggested the use of 37Cl to trap neutrinos) have proposed that neutrinos have a kind of double identity: approximately half the time they are the ordinary ``electron neutrinos'' we suppose them to be but half the time they are ``muon neutrinos.'' Muon neutrinos were discovered at Brookhaven in 1962; they are created by reactions involving the production of muons. They seem to be identical in every way with ordinary electron neutrinos except that when they react with a proton or neutron they produce another muon rather than an electron [see ``The Two-Neutrino Experiment,''by Leon M. Lederman; SCIENTIFIC AMERICAN, March, 1963]. One can also prove that low-energy muon neutrinos will not react with 37Cl. According to Gribov and Pontecorvo, the transformation from one kind of neutrino into another requires times (or distances) that are too large to be obtainable in the laboratory but that are available to neutrinos traveling from the sun to the earth. The neutrinos that arrive in their muon disguise cannot be detected, and thus all capture rates must be divided by a factor of about two. The suggestion made by Gribov and Pontecorvo implies that the minimum capture rate due to pep neutrinos should be reduced. It will not be easy to test this unusual hypothesis, but it cannot be lightly dismissed.
Meanwhile Davis is attempting to improve the sensitivity of his experiment. The improvement, if achieved, should indicate clearly whether the present discrepancy between observation and expectation is due to errors in some experimentally determined parameters used in our solar models or is caused by a basic defect in our theories. Beyond that I believe someone should undertake an experiment using a nuclear species that is more sensitive to low-energy neutrinos than 37Cl. Ordinary lithium, 7Li, is such a nucleus; on capturing a neutrino it yields 7Be and an electron. (This is the reverse of Reaction 6 illustrated in the Proton-Proton Chain) Lithium would respond much better than 37Cl to the pep neutrinos of 1.4 MeV [see illustration on the Predicted Neutrino Capture Rates] and to the low-energy neutrinos produced by the decay of 13N and 15O in the CNO cycle. The combined results of 37Cl and 7Li experiments would constitute a stringent test of present theories of stellar interiors and neutrino reactions. I would not be too surprised to find myself writing another article a few years from now explaining why the results of a successful experiment with 7Li do not agree with our astrophysical expectations.

 Back to John Bahcall's Popular Papers
Back to John Bahcall's Popular Papers